伯恩斯坦多项式与贝塞尔曲线
我们在研究贝塞尔曲线的时候,首先遇到的就是伯恩斯坦多项式(Bernstein polynomial),为此,有必要专门开出一篇文章来探讨伯恩斯坦多项式的性质。当伯恩斯坦系数是二维平面中的一系列固定点时,伯恩斯坦多项式就演变成了贝塞尔曲线。
从定义出发,伯恩斯坦多项式的第n阶项有如下形式:
$$b_{i,n}(t) = \binom{n}{i}\cdot t^{i} \cdot (1-t)^{(n-i)}, \quad t\in[0, 1]$$
其中 i=0, 1, …, n, 而$\binom{n}{i} = \frac{n!}{i!(n-i)!}$是二项式系数。
伯恩斯坦 n 阶多项式可以形成一组 n 阶指数多项式的基底。一般伯恩斯坦多项式可以表示为:
$$B_n(t) = \sum_{i=0}^{n}\beta_i \cdot b_{i, n}(t)$$
其中,$\beta_i$ 叫做伯恩斯坦系数。读者看到这个形式可能一下子就联想到贝塞尔曲线了。是的,这就是贝塞尔曲线的函数形式。
性质
伯恩斯坦多项式满足如下性质:
对称性:$b_{i,n}(t) = b_{n-i,n}(1-t)$
正性:$b_{i,n}(t) \geqslant 0$
归一化:$\sum_{i=0}^{n}b_{i, n}(t) = 1$
极值:
当 $i\neq 0, n$ 时,$b_{i,n}(t)$ 有且只有一个极大值点,位于 $t=\frac{i}{n}$,值为
$b_{i,n}(\frac{i}{n}) = i^i\cdot n^{-n} \cdot (n-i)^{n-i} \binom{n}{i}$
- 临近项关系
伯恩斯坦多项式的项总是可以表示为两个比他高一阶项的线性组合
$b_{i,n-1}(t) = \frac{n-i}{n}b_{i,n}(t) + \frac{i+1}{n}b_{i+1,n}(t)$
而其导数可以表示为两个低一阶项的线性组合
$b_{i,n}^{‘}(t) = n\cdot[b_{i-1,n-1}(t)-b_{i,n-1}(t)]$
当然这里需要考虑到一个约定,即当 i<0 或 i>n 时,$\binom{n}{i} = 0$
这是很容易理解的。二阶项系数的含义是在不考虑顺序的情况下,从 n 中挑选出子集大小为 i 的可能性有多少。当 i<0 或 i>n 时,其可能性当然为零。
由此,我们也知道,当 i<0 或 i>n 时,$b_{i,n}(t) = 0$
- 端点:
当 t=0 或 t=1 时,其结果满足
$\begin{align} b_{i,n}(0) &= \delta_{i, 0} \newline b_{i,n}(1) &= \delta_{i, n} \end{align}$,
其中,$\delta_{i,j} = \begin{cases} 0, &i \neq j \newline 1, &i = j \end{cases}$,是 Kronecker $\delta$ 函数。
- 积分:$\int_{0}^{1} b_{i,n}(t) dt = \frac{1}{n+1}$
多项式前几阶结果
通过求取多项式的前几阶结果,并画出相应的函数图,可以很直观地验证上述伯恩斯坦多项式的几个性质。
零阶:
$\begin{align} b_{0,0}(t) &= 1 \end{align}$
一阶:
$\begin{align} b_{0,1}(t) &= 1-t \newline b_{1,1}(t) &= t \end{align}$
二阶:
$\begin{align} b_{0,2}(t) &= (1-t)^2 \newline b_{1,2}(t) &= 2(1-t)t \newline b_{2,2}(t) &= t^2 \end{align}$
三阶:
$\begin{align} b_{0,3}(t) &= (1-t)^3 \newline b_{1,3}(t) &= 3(1-t)^2t \newline b_{2,3}(t) &= 3(1-t)t^2 \newline b_{3,3}(t) &= t^3 \end{align}$
四阶:
$\begin{align} b_{0, 4}(t) &= (1-t)^4 \newline b_{1, 4}(t) &= 4(1-t)^3t \newline b_{2, 4}(t) &= 6(1-t)^2t^2 \newline b_{3, 4}(t) &= 4(1-t)t^3 \newline b_{4, 4}(t) &= t^4 \end{align}$
五阶:
$\begin{align} b_{0, 5}(t) &= (1-t)^5 \newline b_{1, 5}(t) &= 5(1-t)^4t \newline b_{2, 5}(t) &= 10(1-t)^3t^2 \newline b_{3, 5}(t) &= 10(1-t)^2t^3 \newline b_{4, 5}(t) &= 5(1-t)t^4 \newline b_{5, 5}(t) &= t^5 \end{align}$
贝塞尔曲线
伯恩斯坦多项式的一般形式
$B_n(t) = \sum_{i=0}^{n}\beta_i \cdot b_{i, n}(t)$
其中,$b_{i,n}(t) = \binom{n}{i}\cdot t^{i} \cdot (1-t)^{(n-i)}, \quad t\in[0, 1]$
是 n 阶伯恩斯坦基底多项式。而 $\beta_i$ 叫做伯恩斯坦系数。当伯恩斯坦系数是二维平面中的一系列固定点时,伯恩斯坦多项式就演变成了贝塞尔曲线。
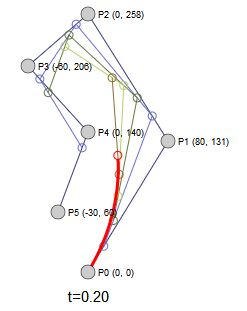
我们先来看一个三阶贝塞尔曲线的例子:
在该例子中,共有四个坐标点(控制点)。读者可以尝试拖动四个控制点,看看贝塞尔曲线的形态变化。
结合伯恩斯坦多项式的前几阶展开式,我们可以得到相应的贝塞尔曲线形式。
线性曲线
对一阶伯恩斯坦多项式展开,得到如下形式:
$B(t) = P_0 \cdot (1-t) + P_1 \cdot t = P_0 + (P_1 – P_0) \cdot t$
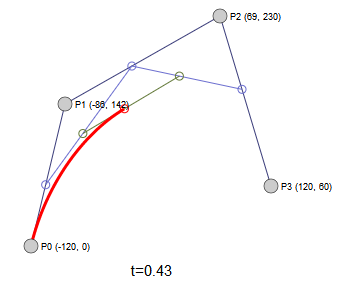
从公式可以看出,二阶展开式对应的是介于 $P_0$和 $P_1$ 之间的线性插值点。其动态效果如下:
二次方曲线
对二阶伯恩斯坦多项式展开,得到如下形式:$B(t) = P_0 \cdot (1-t)^2 + P_1\cdot 2(1-t)t + P_2 \cdot t^2$
B(t) 对 t 求导,得到下式:$B’(t) = 2(1-t)\cdot (P_1 – P_0) + 2t\cdot (P_2 – P_1)$
把两个端点代入式子中:
$$\begin{align} B’(0) &= 2 (P_1 – P_0) \newline B’(1) &= 2 (P_2 – P_1) \end{align}$$
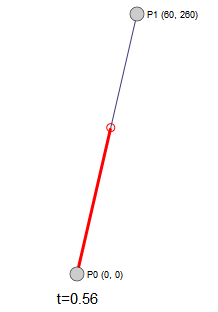
这个结果显示,位于 $P_0$ 和 $P_2$ 点的两条切线相交于 $P_1$ 点。而当 t 从 0 逐渐变化到 1 的过程中, B(t) 点处的切线会从 $P_0P_1$ 直线逐渐过渡到 $P_1P_2$ 直线。其动态效果如下:
读者可以尝试拖动三个坐标点(控制点)看看曲线和切线的形态变化。
三次方曲线
和二次方曲线类似,我们先写出展开式:
$B(t) = P_0 \cdot (1-t)^3 + P_1\cdot 3(1-t)^2t + P_2 \cdot 3(1-t)t^2 + P_3 \cdot t^3$
接着对展开式求导,得到如下结果:
$B’(t) = 3(1-t)^2\cdot (P_1 – P_0) + 6(1-t)t\cdot (P_2 – P_1) + 3t^2\cdot(P_3 – P_2)$
代入端点值:
$\begin{align} B’(0) &= 3 (P_1 – P_0) \newline B’(1) &= 3 (P_3 – P_2) \end{align}$
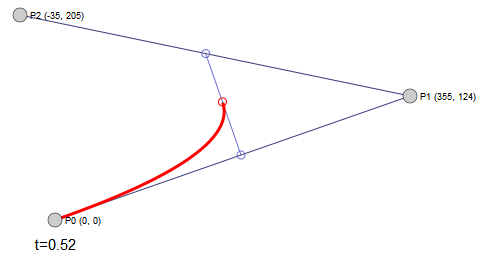
结果显示,位于 $P_0$和 $P_2$ 点的两条切线分别相交于 $P_1$ 点和 $P_2$ 点。而当 t 从 0 逐渐变化到 1 的过程中,B(t) 点处的切线会从 $P_0P_1$直线逐渐过渡到 $P_2P_3$ 直线。其动态效果如下:
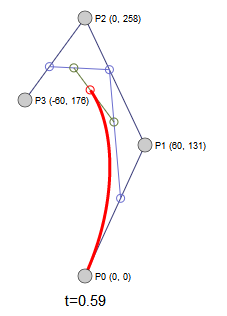
读者同样可以尝试拖动四个坐标点(控制点)来看看曲线和切线的形态变化。
四次方曲线和更高次的曲线,我们不做详细的讨论,只做动态曲线演示。其结论的推导方式和三次方、二次方曲线类似。感兴趣的读者可以自己推导。
四次方曲线
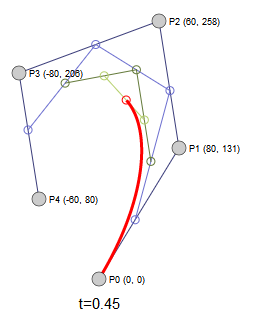
五次方曲线